Chapter 21 Regularized Generalized linear models (glmnet)
In linear regression, the outcome is a linear function of the predictor variables. \[ y = y_0 + c_1 x_1 + c_2 x_2 + c_3 x_3 + \dots \] where \(c_i\) are the coefficients and \(y_0\) is the intercept.
Generalized linear models (GLMs) extend this idea by adding a link function to the outcome variable. \[ g(y) = y_0 + c_1 x_1 + c_2 x_2 + c_3 x_3 + \dots \] Here, \(g\) is the link function. The normal linear regression model uses the identity function \(g(x) = x\). For logistic regression, the link function is \(g(x) = \ln\frac{x}{1-x}\).
21.1 GLM implementation glmnet
The standard R distriution includes the glm function for fitting GLMs. The glmnet package extends this to include L1 and L2 regularization. To be more specific, it solves the following problem:
\[
\min_{\beta_0,\beta} \frac{1}{N}
\sum_{i=1}^{N} w_i l(y_i,\beta_0+\beta^T x_i) +
\lambda\left[\frac{1-\alpha}{2}\|\beta\|_2^2 +
\alpha \|\beta\|_1\right],
\]
Here \(l\) is the negative log-likelihood contribution for observations. The weights \(w_i\) are used to account for sampling weights. The regularization parameters \(\lambda\) and \(\alpha\) are controlling regularization. The \(\lambda\) value controls the strength of the penalty. The type of regularization is defined by the \(\alpha\) value. For \(\alpha=0\), the penalty is L2 regularization (Euclidean norm \(\|\beta\|_2^2\)). For \(\alpha=1\), the penalty is L1 regularization (absolute value norm \(\|\beta\|_1\)). Setting \(\alpha\) to a value between 0 and 1 results in a combination of L1 and L2 regularization. Hastie et al. write about the role of \(\alpha\):
It is known that the ridge penalty shrinks the coefficients of correlated predictors towards each other while the lasso tends to pick one of them and discard the others. The elastic net penalty mixes these two: if predictors are correlated in groups, an \(\alpha=0.5\) tends to either select or leave out the entire group of features. This is a higher level parameter, and users might pick a value upfront or experiment with a few different values. One use of \(\alpha\) is for numerical stability; for example, the elastic net with \(\alpha=1-\epsilon\) for some small \(\epsilon>0\) performs much like the lasso, but removes any degeneracies and wild behavior caused by extreme correlations.
21.2 glmnet in tidymodels
The glmnet package is accessible in the tidymodels framework. It can be selected as an engine for linear regression (see 27.2.3) and logistic regression (see 27.4.2).
The \(\lambda\) parameter in the elasticnet equation corresponds to the penalty argument. \(\alpha\) is controlled by the mixture argument.
You can find example code for using glmnet in the tidymodels in Chapter @ef(model-tuning) and Section @(tune-one-standard-error). Here, we will cover functionality that is specific to glmnet.
Load the packages we need for this chapter.
Let’s start with training a Lasso model on the mtcars dataset.
Code
21.2.1 Coefficients - one of many
We can get the coefficients from the model using the tidy function.
##
## Attaching package: 'Matrix'## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpack## Loaded glmnet 4.1-8## # A tibble: 11 × 3
## term estimate penalty
## <chr> <dbl> <dbl>
## 1 (Intercept) 35.3 1
## 2 cyl -0.872 1
## 3 disp 0 1
## 4 hp -0.0101 1
## 5 drat 0 1
## 6 wt -2.59 1
## 7 qsec 0 1
## 8 vs 0 1
## 9 am 0 1
## 10 gear 0 1
## 11 carb 0 1These are the coefficients of the model corresponding to the penalty of 1. We can see that most coefficients are 0. This is the effect of the L1 regularization.
Under the hood, glmnet is using a grid of \(\lambda\) values and fits the model for all of these values. We can get the coefficients for all examined \(\lambda\) values using the extract_fit_engine function.
## # A tibble: 640 × 5
## term step estimate lambda dev.ratio
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1 20.1 5.15 0
## 2 (Intercept) 2 21.6 4.69 0.129
## 3 (Intercept) 3 23.2 4.27 0.248
## 4 (Intercept) 4 24.7 3.89 0.347
## 5 (Intercept) 5 26.0 3.55 0.429
## 6 (Intercept) 6 27.2 3.23 0.497
## 7 (Intercept) 7 28.4 2.95 0.554
## 8 (Intercept) 8 29.4 2.68 0.601
## 9 (Intercept) 9 30.3 2.45 0.640
## 10 (Intercept) 10 31.1 2.23 0.673
## # ℹ 630 more rowsHere are the results for a lambda value close to 1.
## # A tibble: 4 × 5
## term step estimate lambda dev.ratio
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 18 35.1 1.06 0.805
## 2 cyl 18 -0.868 1.06 0.805
## 3 hp 18 -0.00965 1.06 0.805
## 4 wt 18 -2.56 1.06 0.805The coefficients are the close to the ones we got from the tidy function. glmnet interpolates the coefficients for the \(\lambda\) values that are not in the grid.
21.2.2 Plotting the coefficients
Because the coefficients are all estimated for a grid of \(\lambda\) values, we can plot the coefficients as a function of \(\lambda\). The glmnet package provides a function for this. Figure 21.1 shows the resulting plot.
Code
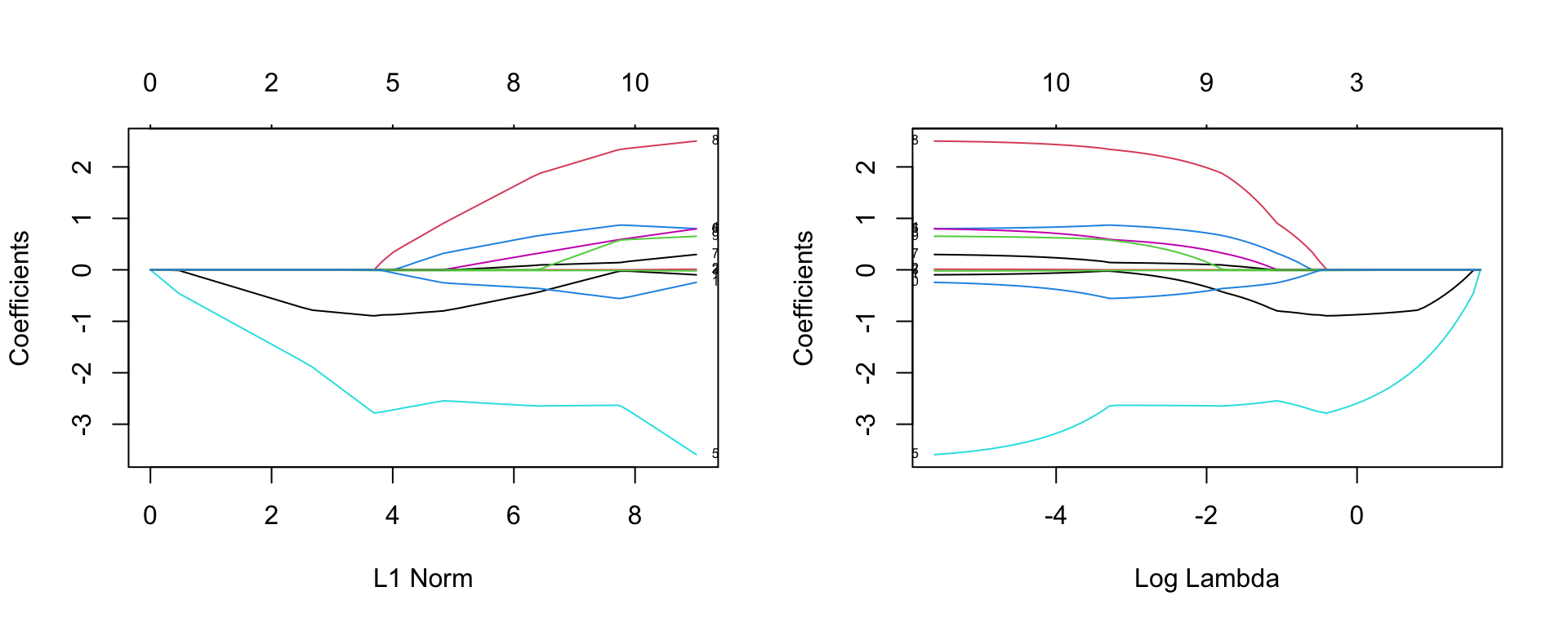
Figure 21.1: Coefficients for the glmnet model as a function of the penalty parameter \(\lambda\).
Each line corresponds to the coefficient value for a given L1 norm of the coefficients. On the left side, all coefficients are 0 due to a very high penalty. As the penalty decreases, the L1 norm increases and we see coefficients different from zero. The numbers on the top of the plot are the number of non-zero coefficients.
Note that the logarithm of lambda used in the right plots is the natural logarithm. This means that for example log lambda of -2 corresponds to lambda of 0.135.
The ggfortify package provides a autoplot function for glmnet models that produces a clearer version of the.
Code
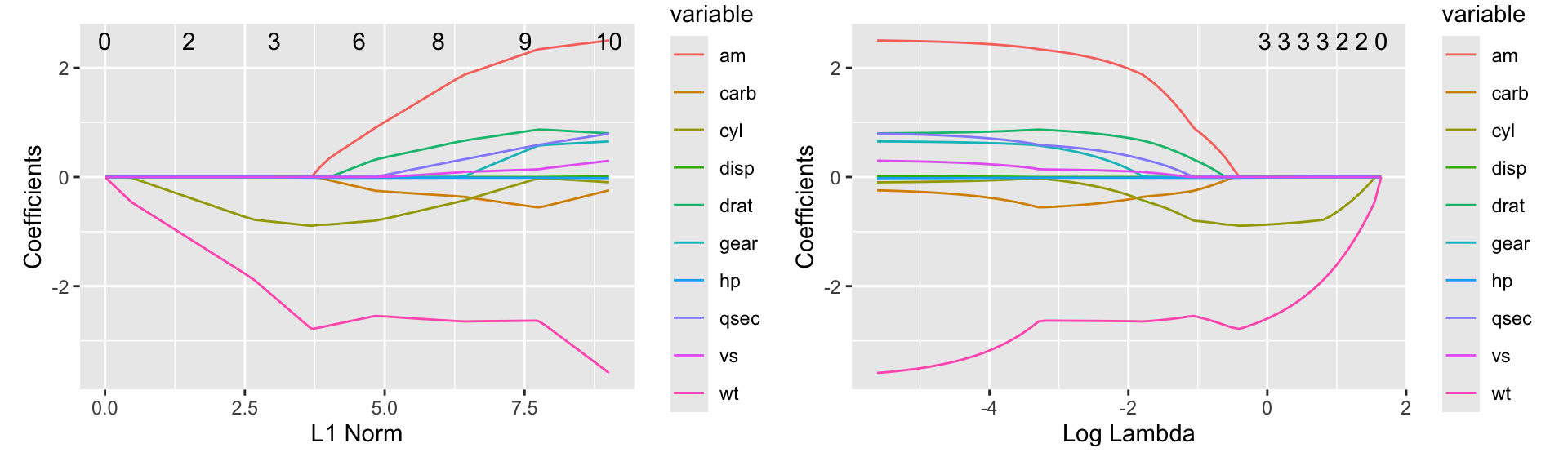
Figure 21.2: Coefficients for the glmnet model using the autoplot function from ggfortify as a function of L1 norm (left) or lambda (right)
Figure 21.2 shows the resulting plot. The left plot shows the coefficients as a function of the L1 norm. The right plot shows the coefficients as a function of the log of the \(\lambda\) value.
Further information:
Code
The code of this chapter is summarized here.
Code
knitr::opts_chunk$set(echo=TRUE, cache=TRUE, autodep=TRUE, fig.align="center")
library(tidymodels)
library(tidyverse)
library(ggfortify)
library(patchwork)
set.seed(123)
rec <- recipe(mpg ~ ., data=mtcars)
spec <- linear_reg(mode="regression", penalty=1.0, mixture=1) %>%
set_engine("glmnet")
wf <- workflow() %>%
add_recipe(rec) %>%
add_model(spec)
wf_fit <- wf %>% fit(mtcars)
tidy(wf_fit)
tidy(wf_fit %>% extract_fit_engine())
wf_fit %>%
extract_fit_engine() %>%
tidy() %>%
filter(lambda < 1.1) %>%
filter(lambda >= 1.0)
opar <- par(mfrow=c(1, 2))
plot(wf_fit %>% extract_fit_engine(), label=TRUE)
plot(wf_fit %>% extract_fit_engine(), label=TRUE, xvar="lambda")
par(opar)
g1 <- autoplot(wf_fit %>% extract_fit_engine(), xvar="norm")
g2 <- autoplot(wf_fit %>% extract_fit_engine(), xvar="lambda")
g1 + g2